FMCW 雷达原理

连续波雷达（CW Radar）测速原理

连续波雷达测速度的核心原理是多普勒效应，即目标沿雷达径向运动时，回波频率会发生偏移。下面是公式推导：

① 发射信号

假设雷达发射一个连续正弦波信号：

stx(t)=Acos⁡(2πfct)s_{\rm tx}(t) = A \cos(2 \pi f_c t)

其中，fcf_c 为雷达载波频率，AA 为信号幅度。

② 回波信号

若目标距离为 R(t)R(t)，则回波会有延迟 τ(t)\tau(t)，如下：

τ(t)=2R(t)c\tau(t) = \frac{2 R(t)}{c}

回波信号为：

srx(t)=Arcos⁡(2πfc(t−τ(t)))s_{\rm rx}(t) = A_r \cos \big( 2\pi f_c (t - \tau(t)) \big)

其中 ArA_r 是回波幅度，考虑到距离衰减和目标反射。

③ 目标运动

假设目标沿径向速度为 vv，以正向远离雷达为正，则：

R(t)=R0+vt⇒τ(t)=2(R0+vt)cR(t) = R_0 + v t \quad \Rightarrow \quad \tau(t) = \frac{2(R_0 + v t)}{c}

将 τ(t)\tau(t) 代入回波信号：

srx(t)=Arcos⁡[2πfc(t−2(R0+vt)c)]=Arcos⁡[2πfct−4πfcc(R0+vt)]=Arcos⁡[2π(fc−2vλ)t−4πfcR0c]\begin{aligned} s_{\rm rx}(t) &= A_r \cos \Big[ 2 \pi f_c \Big( t - \frac{2(R_0 + v t)}{c} \Big) \Big] \\ &= A_r \cos \Big[ 2 \pi f_c t - \frac{4 \pi f_c}{c} (R_0 + v t) \Big] \\ &= A_r \cos \Big[ 2 \pi \Big(f_c - \frac{2 v}{\lambda}\Big) t - \frac{4 \pi f_c R_0}{c} \Big] \end{aligned}

注：波长 λ=c/fc\lambda = c / f_c

④ 多普勒频移

通过上面公式推导，可以得出，回波信号的瞬时频率为：

frx=fc−2vλf_{\rm rx} = f_c - \frac{2v}{\lambda}

与发射信号的频率相比，频率偏移为：

fD=2vλf_D = \frac{2v}{\lambda}

从而通过解出速度，如下：

v=λfD2v = \frac{\lambda f_D}{2}

特别说明

普通连续波雷达没有发射脉冲，不知道信号何时返回，无法测量距离。 若要测距，需要对连续波进行调制，例如线性调频（FMCW）或脉冲调制。

FMCW 雷达：锯齿波测距原理

FMCW雷达是在CW基础上叠加频率调制，常见形式是锯齿波调频，下面是推导过程：

① 发射信号

假设单次线性频率调制在区间 0≤t≤Tc0\le t\le T_c内上升，瞬时频率为：

ftx(t)=fc+ktf_{\text{tx}}(t)=f_c + k t

其中 fcf_c 为起始载波频率，kk 为调频斜率（Hz/s）。若单次扫频带宽为 BB，则 k=B/Tck=B/T_c

对应的瞬时相位（取相位相对于 t=0t=0 的积分）：

ϕtx(t)=2π∫0tftx(τ) dτ=2π(fct+12kt2)\phi_{\text{tx}}(t)=2\pi\int_0^t f_{\text{tx}}(\tau)\,d\tau =2\pi\Big(f_c t + \tfrac{1}{2} k t^2\Big)

于是，复包络为：

stx(t)=ejϕtx(t)=ej2π(fct+12kt2)s_{\text{tx}}(t)=e^{j\phi_{\text{tx}}(t)}=e^{j2\pi(f_c t + \tfrac12 k t^2)}

② 回波信号

目标与雷达的往返时延为

τ=2Rc\tau=\frac{2R}{c}

回波是发射信号的延迟、衰减并带相移的版本，复包络可写为

srx(t)=A ejϕtx(t−τ)=A ej2π(fc(t−τ)+12k(t−τ)2)s_{\text{rx}}(t)=A\,e^{j\phi_{\text{tx}}(t-\tau)} = A\,e^{j2\pi\big(f_c (t-\tau) + \tfrac12 k (t-\tau)^2\big)}

其中，AA 含衰减与反射。

③ 混频

接收机通常将回波与本地发射信号相乘并低通滤波（或与发射的共轭相乘），即取

smix(t)=srx(t)⋅stx∗(t)=A ej(ϕtx(t−τ)−ϕtx(t))s_{\text{mix}}(t)=s_{\text{rx}}(t)\cdot s_{\text{tx}}^*(t) = A\, e^{j(\phi_{\text{tx}}(t-\tau)-\phi_{\text{tx}}(t))}

拍相位为：

ϕb(t)=ϕtx(t−τ)−ϕtx(t)\phi_b(t)=\phi_{\text{tx}}(t-\tau)-\phi_{\text{tx}}(t)

代入相位表达式：

ϕtx(t−τ)=2π(fc(t−τ)+12k(t−τ)2)=2π(fct−fcτ+12kt2−ktτ+12kτ2)\begin{aligned} \phi_{\text{tx}}(t-\tau) &=2\pi\Big(f_c (t-\tau) + \tfrac12 k (t-\tau)^2\Big) \\ &=2\pi\Big(f_c t - f_c\tau + \tfrac12 k t^2 - k t\tau + \tfrac12 k\tau^2\Big) \end{aligned}

而

ϕtx(t)=2π(fct+12kt2)\phi_{\text{tx}}(t)=2\pi(f_c t + \tfrac12 k t^2)

因此，差相位为：

ϕb(t)=ϕtx(t−τ)−ϕtx(t)=2π(−fcτ−ktτ+12kτ2)\begin{aligned} \phi_b(t) &= \phi_{\text{tx}}(t-\tau)-\phi_{\text{tx}}(t) \\ &=2\pi\big(-f_c\tau - k t\tau + \tfrac12 k\tau^2\big) \end{aligned}

常数项 −2πfcτ-2\pi f_c\tau、随 tt 线性增长的项 −2πktτ-2\pi k t\tau、以及与 tt 无关的常数项 +πkτ2+\pi k\tau^2。

于是混频输出为

smix(t)=A ejϕb(t)=Aexp⁡{j2π(−fcτ−ktτ+12kτ2)}s_{\text{mix}}(t)=A\,e^{j\phi_b(t)} = A \exp\big\{ j2\pi(-f_c\tau - k t\tau + \tfrac12 k\tau^2)\big\}

④ 拍频

拍频定义为拍相位对时间的导数除以 2π2\pi：

fb(t)=12πdϕb(t)dtf_b(t)=\frac{1}{2\pi}\frac{d\phi_b(t)}{dt}

对上式求导，也就是对 tt 求导：

dϕbdt=2π(−kτ)⇒fb=−kτ\frac{d\phi_b}{dt}=2\pi(-k\tau) \quad\Rightarrow\quad f_b = -k\tau

取频率的模值，只关系拍频大小：

fb=kτf_b = k\tau

把 τ=2Rc\tau=\dfrac{2R}{c} 带入，得到经典测距关系：

fb=2kRc⟹R=cfb2kf_b = \dfrac{2kR}{c} \quad\Longrightarrow\quad R=\dfrac{c f_b}{2k}

注：符号上的正负只表明相位差的方向，测距时取绝对频率即可。

⑤ 其他表示方法

因为 k=B/Tck=B/T_c，也可写为

R=cfb2k=c Tc2B fbR = \frac{c f_b}{2k} = \frac{c\,T_c}{2B}\, f_b

下面是调频连续波雷达（锯齿波）的原理图：

锯齿形 连续波
图 1：锯齿形调频连续波雷达的测距原理

FMCW 雷达：锯齿波测速原理

FMCW 雷达要实现同时测距和测速，常用的处理方法是二维 FFT（Range-Doppler 处理）：

  • 横向（快时间）FFT → 将每条 chirp 内的拍频转化为距离信息；
  • 纵向（慢时间）FFT → 将多个 chirp 的相位随 chirp 序号的演化转化为速度信息。

① 慢时间信号

对于一个固定距离（即拍频对应的某个距离），从连续多条 chirp 中采样复数值，得到一个关于 chirp 序号 mm 的序列：

s[m]=A ej(2πfDmTc+ϕ0),m=0,1,…,M−1s[m] = A \, e^{j(2\pi f_D m T_c + \phi_0)}, \quad m=0,1,\dots,M-1

其中：TcT_c 为单条 chirp 时长，MM 为连续 chirp 的数量，fD=2vλf_D = \tfrac{2v}{\lambda} 为多普勒频率，ϕ0\phi_0 为初始相位。

直观理解：目标在运动时，每经过一条 chirp，回波相位会在慢时间方向上“逐渐旋转”，形成一个等比相位序列。

② 慢时间 FFT

将 s[m]s[m] 在 mm 方向做 FFT：

S[k]=∑m=0M−1s[m] e−j2πMkm,k=0,1,…,M−1S[k] = \sum_{m=0}^{M-1} s[m] \, e^{-j \tfrac{2\pi}{M} k m}, \quad k=0,1,\dots,M-1

这是对慢时间采样信号的离散频谱分析。

FFT 的峰值出现在

fD≈kMTcf_D \approx \frac{k}{M T_c}

从而可以估计多普勒频率：

f^D=kpeakMTc\hat{f}_D = \frac{k_{\text{peak}}}{M T_c}

由多普勒公式，速度计算为：

v=λf^D2v = \frac{\lambda \hat{f}_D}{2}

FMCW 雷达：三角波测距、测速原理

① 三角波调频

在锯齿波调制中，频率单向线性增加；而 三角波调频 由 上行 chirp（up-chirp） 和 下行 chirp（down-chirp） 构成：

ftx(t)={fc+kt,0≤t<Tc(up-chirp)fc+k(2Tc−t),Tc≤t<2Tc(down-chirp)f_{tx}(t) = \begin{cases} f_c + k t, & 0 \le t < T_c \quad \text{(up-chirp)} \\[6pt] f_c + k (2T_c - t), & T_c \le t < 2T_c \quad \text{(down-chirp)} \end{cases}

其中：

  • k=B/Tck = B/T_c：调频斜率，上行与下行符号相反
  • 一个完整周期包含 up-chirp 与 down-chirp，总时长 2Tc2T_c

② 上行、下行拍频

假设目标相对于雷达移动，信号一方面产生距离的时延，时延影响拍频；另一方面产生速度的多普勒频移，频移也影响拍频。

目标距离 RR、径向速度 vv，对应时延与频移为：

τ=2Rc,fD=2vλ\tau = \frac{2R}{c}, \qquad f_D = \frac{2v}{\lambda}

上行、下行拍频 = 距离引起的拍频 ± 多普勒频移。

  • Up-chirp 拍频：

fb↑=kτ+fDf_b^{\uparrow} = k\tau + f_D

  • Down-chirp 拍频：

fb↓=−kτ+fDf_b^{\downarrow} = -k\tau + f_D

③ 距离、速度解算

将上行、下行的拍频结合，可解耦出 RR 和 vv：

  • 距离（消除多普勒影响）：

R=c4k(fb↑−fb↓)R = \frac{c}{4k} \Big( f_b^{\uparrow} - f_b^{\downarrow} \Big)

  • 速度（消除距离影响）：

v=λ4(fb↑+fb↓)v = \frac{\lambda}{4} \Big( f_b^{\uparrow} + f_b^{\downarrow} \Big)

下面是调频连续波雷达（三角波）的原理图：

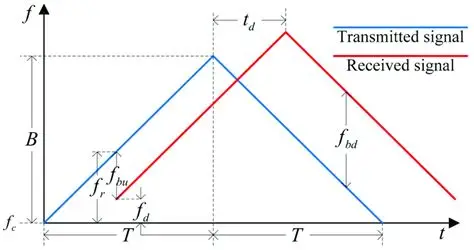
三角形 连续波
图 2：三角形调频连续波雷达的测距原理

性能指标：

  • 距离分辨率

ΔR=c2B\Delta R = \frac{c}{2B}

  • 最大无模糊距离

Rmax⁡=cTc2R_{\max} = \frac{c T_c}{2}

  • 速度分辨率

Δv=λ2MTc\Delta v = \frac{\lambda}{2 M T_c}

  • 最大无模糊速度

vmax⁡=λ4Tcv_{\max} = \frac{\lambda}{4 T_c}